Compactness
A contributed talk (of 25 minutes) at the Caucasian Mathematics Conference, Tbilisi, Georgia, September 5 and 6, 2014.
The talk was intended to be part of the Algebra and Model Theory
session organized by Tuna Altınel and Ayşe Berkman. As it turned out,
this session
was required to be two parallel sessions, because
participation was made open to all by the conference organizers.
My talk was chaired by Tuna on Friday, September 5. I had expected or at least hoped that non-model-theorists would be in the audience, and I had prepared my talk accordingly; in the event, my audience consisted only of model-theorists from Istanbul, like me.
- Abstract
-
This is a general talk on the interplay of logic, algebra, and topology. The starting point is an occasional confusion in model theory about the Compactness Theorem. The name of this theorem is sometimes explained as deriving from the compactness of a certain Stone space. This explanation is misleading, since all Stone spaces are compact. In the most general sense, a logic can be understood as a relation of truth, connecting certain structures to certain sentences. The truth relation establishes a Galois correspondence between classes of structures and sets of sentences. The set of all sentences can be replaced by a quotient, which is usually a Boolean algebra. Then a topology is induced on the class of structures, and the Kolmogorov quotient of this class embeds in the Stone space of the Boolean algebra of sentences. In general, the embedding might be proper. In first-order logic (and, under a further restriction, in no other logic, by Lindström's Theorem), this embedding is a bijection: this is the Compactness Theorem. Equivalently, the image of the embedding is dense and closed; and then Łoś's Theorem on ultraproducts is just an explicit way of establishing this closedness—albeit a way that relies on the full Axiom of Choice, or equivalently the Maximal Ideal Theorem, rather than the weaker Prime Ideal Theorem, which is equivalent to the Compactness Theorem as such.
- Slides
I made changes to my slides until the last morning. They are 16 pages, including title page.
- Note
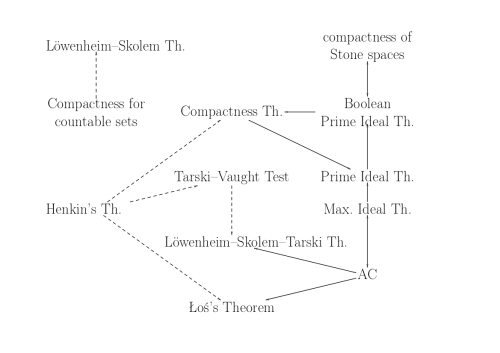
The diagram above is from the third slide. It transpired during the talk that the two different kinds of arrows were confusing.
The solid arrows denote logical implication in ZF set theory.
Each broken arrow points from a theorem to a corollary.
The relation between a theorem and a corollary is merely rhetorical: to say that B is a corollary of A means simply that, once you have proved A, then it is easy to prove B. By contrast, a logical implication may be quite difficult to prove. Indeed, just about all theorems of ordinary mathematics are equivalent to one another in ZF set theory with the Axiom of Choice; but proving this normally just means proving all of the theorems in the usual way.
I made the diagram with Xy-pic. Unfortunately the arrowheads didn't scale up with the ordinary letters. I think they can be made to scale; but they could not by me.
- Notes
Just some notes I made for my own use while preparing the talk.