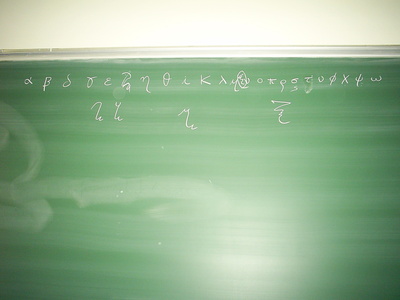Ancient Greek Mathematics
Math 303, METU, Fall semester, 2009
If you cannot read all of the Greek letters on this page, please inform me.
Practicalities
- Weekly schedule:
- Tuesdays, 16.40--17.30; Fridays, 15.40--17.30; in M-105
- Instructor:
- David Pierce
- Official title of course:
- HISTORY OF MATHEMATICAL CONCEPTS I
Exams
- November 6:
- January 12 (the final exam; 4 pp.):
The day after the first exam, in a nearby classroom, I noticed an attempt at writing the Greek alphabet on a blackboard:
The photograph shows a few mistakes:
- γ and δ are transposed;
- ξ should come after ν;
- ι should not have a dot;
- ζ and ξ might be drawn more carefully.
- μ seems to be reversed.
You might be amused by the Evolution of Alphabets page: check out in particular the evolutions of the Greek from Phoenician, and Latin from Greek alphabet.
About the course
I prefer the title "History of Mathematics I" or rather "Ancient Greek Mathematics." We shall read some texts written originally in ancient Greek, starting with Euclid's Elements, perhaps moving on to Archimedes and Apollonius. I do not expect to treat every topic in the catalogue description of the course.
Added, January 8, 2009: Indeed, what we have covered is:
- Euclid's Elements:
- Book I (all)
- Book II, propositions 1–5
- Book III, propositions 1–3, 20, 21, 22, 31
- Book V, propositions 1, 2, 4, 7–9, 11, 12, 14–18, 20, 22
- Book VI, propositions 1, 2, 4, 6, 8, 11, 12, 15–19
- Book XI, propositions 1–6, 8–10, 14–16, 18
- The Conics of Apollonius: Book 1, propositions 1–21
Class attendance is required. Attendence will be reflected in grades according to the catalogue scheme. For example, no student can get a grade of CC or higher unless the student attends at least 70% of the hours of the class.
Class participation is also required. In class, students will present the theorems and proofs of Euclid at the board, in English. At the beginning, all students should be able to prove all of Euclid's theorems, without notes.
There will be a midterm (in class on November 6) and a final exam.
I also ask students to learn, in order, the 24 letters of the Greek alphabet, and to able to recognize some of the Greek words that have become technical terms in mathematics today. You can get the letters from Wikipedia for example, or from a sheet prepared by me, as a pdf, ps, or dvi file. (The LaTeX file is also available, but few people will have the Greek fonts installed.)
Texts
Euclid
The text of Euclid's Elements begins with definitions, postulates, and "common notions". Probably at least some of the definitions were not in Euclid's original text. (See Lucio Russo, The Forgotten Revolution, 10.15, pp. 320–7.)
The text of the Elements is available in various versions.
Original Greek
The Greek text established by J. L. Heiberg is available from the Perseus Collection or its Berlin mirror. A scan of the original print edition is available from wilbourhall.org.Heath
The English translation and commentary of T. L. Heath are also available from the Perseus Collection or its Berlin mirror.
Heath's original three-volume print edition of the Elements, originally published by Cambridge in 1908, has been reissued by Dover Publications. Again, a scan of the original print edition is also available from wilbourhall.org.
Heath's translation by itself (without the extensive but distracting commentary) is published by Green Lion Press.
Fitzpatrick
The Greek text with parallel English translation (and a few footnotes) by Richard Fitzpatrick (2008) is available as a pdf file from the translator's website.
Joyce
There is an English text with applets prepared by David E. Joyce, 1998. (The text is said to be "similar" to Heath's English version. Modern commentary is added.)
Apollonius
Book I of Taliaferro's translation in the Green Lion Press edition is in the library photocopy shop.
The translation of Rosenfeld is available on line. It claims to be more faithful to the Greek than the Taliaferro. Unfortunately it does not have diagrams: the reader is invited to use the diagrams of Heiberg's text:
The Greek text established by Heiberg, with his Latin translation facing, can be found through the Wilbour Hall website.
Heath's version of Apollonius is also available through Wilbour Hall; it is not a translation, but a rewriting in modern terms.
Ancillary notes
I prepared some general comments about ancient mathematics, including why it is worth studying (10 pp.):
Additional notes follow.
Euclid does not discuss his work, and in particular he does not use the word γεωμετρία. Herodotus does use the word, a century or two earlier. This is Herodotus of Halicarnassus, today's Bodrum: in Book II, Chapter 109, of his great historical work, he writes:
For this cause Egypt was intersected [by canals]. This king [Sesostris] moreover (so they said) divided the country among all the Egyptians by giving each an equal square parcel of land, and made this his source of revenue, appointing the payment of a yearly tax. And any man who was robbed by the river of a part of his land would come to Sesostris and declare what had befallen him; then the king would send men to look into it and measure the space by which the land was diminished, so that thereafter it should pay in proportion to the tax originally imposed. From this, to my way of thinking, the Greeks learnt the art of measuring land [γεωμετρίη]; the sunclock [πόλος] and the sundial [γνώμων], and the twelve divisions of the day, came to Hellas not from Egypt but from Babylonia.
Such is the translation of A. D. Godley (Herodotus, The Persian Wars, Loeb Classical Library, Harvard University Press, revised 1926). For γεωμετρίη (the Ionic form of the word) here, other translators, as Aubrey de Sélincourt (Herodotus, The Histories, Penguin Classics, revised 1972), just use geometry. It is too simple to say that geometry developed from surveying, since it was not necessary for geometry as we know it to develop at all. After all, Euclid was under no external obligation to create the Elements.
Our word mathematics comes ultimately from the Greek verb μανθάνω learn. A noun derived from this, μάθημα that which is learnt, appears in the plural (μαθήματα) in Herotodus (I.207). The speaker is Croesus, who had been king of Lydia, in western Anatolia, before his defeat by the Persians:
This is translated by Godley as “Disaster has been my teacher”; and by de Sélincourt as “I have learnt much from my own cruel misfortunes.”τὰ δὲ μοι παθήματα ἐόντα ἀχάριτα μαθήματα γέγονε.
A poem
Euclid Alone Has Looked on Beauty BareEuclid alone has looked on Beauty bare.
Let all who prate of Beauty hold their peace,
And lay them prone upon the earth and cease
To ponder on themselves, the while they stare
At nothing, intricately drawn nowhere
In shapes of shifting lineage; let geese
Gabble and hiss, but heroes seek release
From dusty bondage into luminous air.O blinding hour, O holy, terrible day,
When first the shaft into his vision shone
Of light anatomized! Euclid alone
Has looked on Beauty bare. Fortunate they
Who, though once only and then but far away,
Have heard her massive sandal set on stone.—Edna St. Vincent Millay, 1892–1950
Notes on Propositions I.1–3 of Euclid
I summarize some of Euclid's propositions in my own words, and make some remarks.
PROPOSITION 1. To construct, on a given straight line, an equilateral triangle.
Solution. Let AB be the given straight line. Draw two circles, one with center A and passing through B, and the other with center B, passing through A. The circles meet at a point C. Draw the straight lines AC and BC. Then ABC is the desired triangle.
The Greek for line is γραμμή "stroke of a pen", from γράφω "scratch, draw, write". A line in this sense may be curved. It usually has endpoints, πέρατα (singular πέρας "end, limit, boundary"). A straight line is εὐθεῖα γραμμή, or simply εὐθεῖα "straight".
Proposition 1 is more precisely a problem (πρόβλημα, from προβάλλω "throw forward"), as opposed to a theorem (θεώρημα "sight, object of contemplation", from θεάομαι "behold, contemplate"). A problem is something to do; a theorem is something to see.
The solution of the problem assumes that a circle (κύκλος) can be drawn with a given center (κέντρον), passing through a given point. (More precisely, the circumference [περιφέρεια] of the circle will pass through the given point.) That such a circle can be constructed is Euclid's Postulate 3.
The solution also assumes that a straight line can be drawn from any point (σημεῖον "mark [by which something is known]") to any other point: this is Postulate 1.
Finally, the solution assumes that the two circles meet. This is not an explicit postulate in the text that we have.
PROPOSITION 2. To place at a given point a straight line equal to a given straight line.
Solution. Let A be the point; BC, the straight line. Draw AB and construct on this an equilateral triangle, ABD [using Prop. 1]. Draw a circle with center B, passing through C. Extend DB beyond B to meet the circle at E. Draw a circle with center D, passing through E. Extend DA beyond A to meet this circle at F. Since DE and DF are equal, and DB and DA are equal, the remainders BE and AF are equal. Also BC and BE are equal. Hence AF and BC are equal. So AF is as desired.
We have used Postulate 2.
We have used that a straight line through the center of a circle can be extended to meet the circle; but this might be considered as part of the definition of a circle.
We have used "Common Notions" 1 and 3; but the inclusion of these in the Elements may not have been by Euclid (Russo p. 39, n. 29).
PROPOSITION 3. Given two unequal straight lines, to cut off from the greater a part equal to the less.
Solution. Let AB be the greater; C, the less. Draw AD equal to C [Prop. 2]. Draw a circle with center A, passing through D. The circle meets AB at a point, E. Then AE is a part of AB equal to AD and hence to C.
We now can work with a "fixable" compass (or pair of compasses). Before we only had a "collapsible" compass; once we picked it up off the paper, the distance between the ends was lost.
A poem
A Valediction: Forbidding MourningAs virtuous men passe mildly away,
And whisper to their soules, to goe,
Whilst some of their sad friends doe say
The breath goes now, and some say, no:So let us melt, and make no noise,
No teare-floods, nor sigh-tempests move,
T'were profanation of our joyes
To tell the layetie our love.Moving of th'earth brings harmes and feares,
Men reckon what it did and meant,
But trepidation of the spheres,
Though greater farre, is innocent.Dull sublunary lovers love
(Whose soule is sense) cannot admit
Absence, because it doth remove
Those things which elemented it.But we by a love so much refin'd
That our selves know not what it is,
Inter-assured of the mind,
Care lesse, eyes, lips, and hands to misse.Our two souls therefore, which are one,
Though I must goe, endure not yet
A breach, but an expansion,
Like gold to ayery thinnesse beat.If they be two, they are two so
As stiff twin compasses are two;
Thy soul, the fixt foot, makes no show
To move, but doth, if the'other doe.And though it in the center sit,
Yet when the other far doth rome,
It leans and hearkens after it,
And growes erect, as that comes home.Such wilt thou be to mee, who must
Like th'other foot, obliquely run;
Thy firmnes makes my circle just,
And makes me end where I begunne.—John Donne (1572–1631)
I.4
PROPOSITION 4 [SAS]. If two sides of a triangle are equal respectively to two sides of another, and the included angles are equal, then the triangles are equal in all respects (that is, the third sides are equal, and the angles opposite the equal sides are equal, and the triangles themselves are equal [in area].Proof. Let AB and AC be equal respectively to DE and DF, and angle BAC be equal to EDF. Then triangle ABC can be applied to DEF so that A lies on D, and AB on DE, and AC on DF. Then BC lies on EF. So the two triangles can be made to coincide and are therefore equal in all respects.
This proposition is a theorem. The possibility of applying one figure to another is implicit in Common Notion 4: Things which coincide with one another are equal to one another. Proposition 4 uses a sort of converse of this: Things that are equal can be made to coincide. Note also the assumption that two distinct straight lines cannot have common endpoints. This can be taken as a consequence of Postulate 1; but some texts apparently insert the observation here.
Euclid refers to equality of the triangles, not equality of their areas. However, in Proposition 35, it is shown that two parallelograms may be equal [in area], though they are not equal, as I say, in all respects.